В этой статье мы расскажем о матрицах в Python и о том, как создать матрицу с помощью массивов. Затем мы рассмотрим различные методы и примеры операций с матрицами для лучшего понимания этой технологии.
Что такое матрица
В целом, матрица представляет собой таблицу чисел, которую используют в математике и инженерных науках для отображения данных. Она организована в виде таблицы, где есть строки и столбцы. Каждый элемент матрицы имеет уникальный индекс, определяемый номером строки и столбца, в котором он расположен.
Матрица в Python представляет собой прямоугольный массив Numpy. Этот массив должен быть двумерным. Он содержит данные, которые хранятся в строках и столбцах массива.
В матрице Python горизонтальные последовательности элементов называются «строками», а вертикальные последовательности элементов – «столбцами». Строки и столбцы стекаются друг на друга, подобно вложенному списку. Если матрица содержит r-количество строк и c-количество столбцов (где r и c – положительные целые числа), то r х c определяет порядок этого объекта матрицы.
В матрице вы можете хранить строки, целые числа и объекты других типов данных. Данные хранятся в стопках строк и столбцов.
Матрица – это важная структура данных для вычислений в математике и науке. В Python как матрицу рассматривают список списков или вложенный список, поскольку этому языку не свойственны встроенные типы матрицы.
Как создать матрицу в Python
В Python есть несколько способов формирования матрицы, и вот некоторые из них:
- С использованием списков. Можно создать матрицу, воспользовавшись вложенными списками. Каждый вложенный список соответствует одной строке матрицы.
Пример создания квадратной матрицы в Python:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
● С использованием NumPy. NumPy – это библиотека для математических вычислений и обработки данных. В ней существует класс Array, который позволяет создавать матрицы.
Пример использования NumPy для создания матрицы:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
Если вам требуется выполнять стандартные математические операции с матрицами, мы рекомендуем использовать NumPy. Это более удобно, поскольку все операции уже реализованы в библиотеке.
Однако, если вам необходимо создавать собственные методы, например, в образовательных целях, или если планируете проводить нестандартные манипуляции, тогда лучше воспользоваться вложенными списками.
Матричные операции
Матричные операции представляют собой различные действия, которые можно выполнять с матрицами. Теперь давайте рассмотрим различные операции и проведем их с использованием как вложенных списков, так и NumPy.
Сложение
В Python сложение матриц осуществляется путем сложения соответствующих элементов матриц. Если у вас есть две матрицы A и B одинакового размера, то результат сложения матриц C будет матрицей, где каждый элемент C[i][j] равен сумме A[i][j] и B[i][j].
Необходимо помнить, что при сложении двух матриц их размеры должны быть одинаковыми.
Вот пример сложения матриц с использованием вложенных списков и циклов:
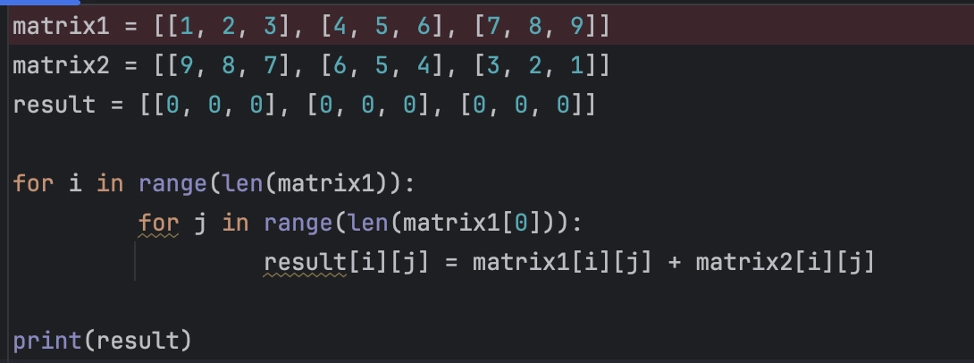
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] + matrix2[i][j]
print(result)
Вывод:
[[10, 10, 10], [10, 10, 10], [10, 10, 10]]

Аналогичное сложение можно выполнить с использованием метода «add()» из библиотеки NumPy:
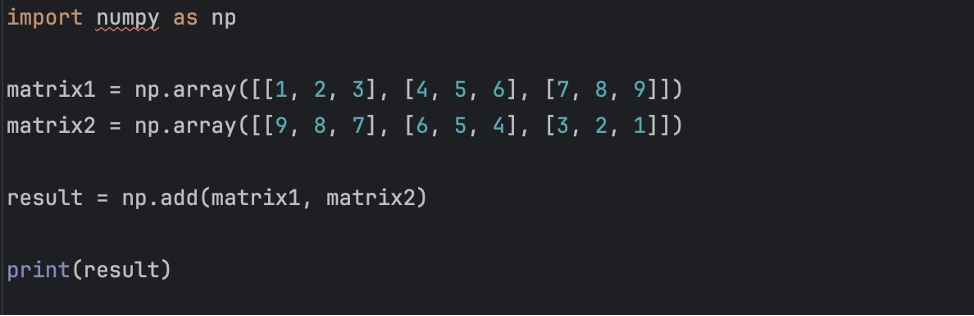
import numpy as np
matrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
result = np.add(matrix1, matrix2)
print(result)
Вывод:
[[10, 10, 10], [10, 10, 10], [10, 10, 10]]
Вычитание
Вычитание матриц в математике и программировании подразумевает вычитание соответствующих элементов одной матрицы из соответствующих элементов другой матрицы. Если у вас есть две матрицы A и B одинакового размера, то результат вычитания матриц C будет матрицей, где каждый элемент C[i][j] равен разности A[i][j] и B[i][j].
В Python вы можете выполнять вычитание матриц с использованием цикла или метода «subtract()» из библиотеки NumPy. При этом размеры матриц должны быть одинаковыми.
Пример вычитания с использованием цикла:
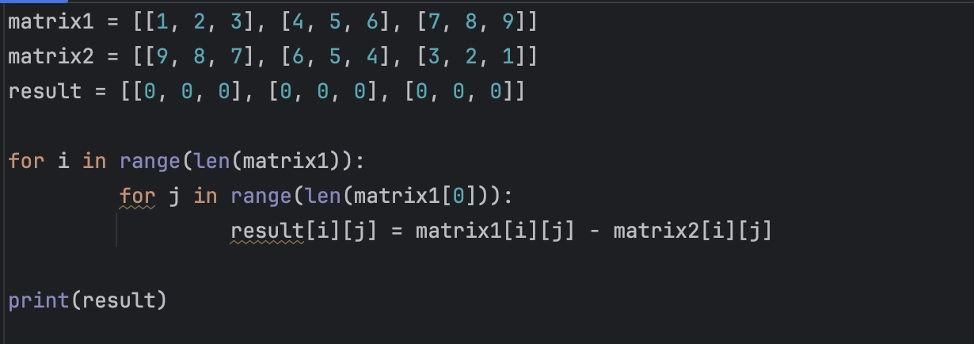
matrix1 = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
matrix2 = [[9, 8, 7], [6, 5, 4], [3, 2, 1]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix1[0])):
result[i][j] = matrix1[i][j] - matrix2[i][j]
print(result)
Вывод:
[[-8, -6, -4], [-2, 0, 2], [4, 6, 8]]

Вычитание с использованием метода «subtract()» из библиотеки NumPy:
import numpy as np
matrix1 = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
matrix2 = np.array([[9, 8, 7], [6, 5, 4], [3, 2, 1]])
result = np.subtract(matrix1, matrix2)
print(result)

Вывод:
[[-8, -6, -4], [-2, 0, 2], [4, 6, 8]]
Умножение на число
Умножение матрицы на число означает умножение каждого элемента матрицы на это число. Если у вас есть матрица A и число k, то результатом умножения будет новая матрица C, где каждый элемент C[i][j] равен произведению k и A[i][j].
В Python умножение матрицы на число можно осуществить с использованием цикла или с использованием метода «dot()» из библиотеки NumPy.
При умножении матрицы на число каждый элемент умножается на это число.
Пример умножения с использованием цикла:
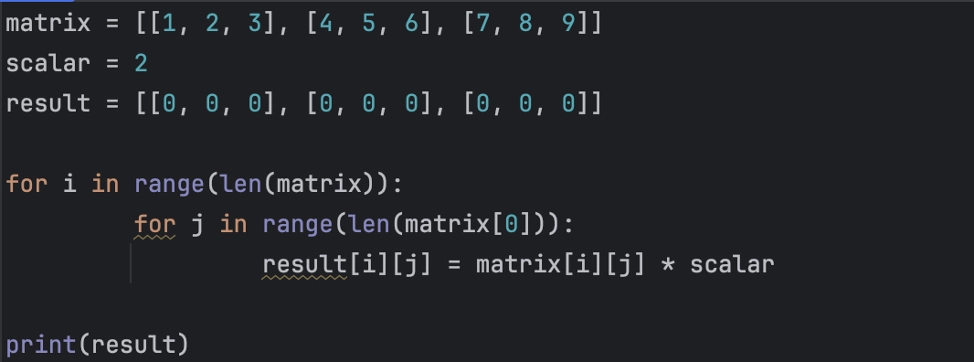
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
scalar = 2
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[i][j] = matrix[i][j] * scalar
print(result)
Вывод:
[[2, 4, 6], [8, 10, 12], [14, 16, 18]]

Пример работы метода «dot()» из библиотеки NumPy с теми же входными данными:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2
result = np.dot(matrix, scalar)
print(result)

Вывод:
[[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]]
Также вместо метода «dot()» можно использовать знак операции умножения «*»:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
scalar = 2
result = matrix * scalar
print(result)

Вывод:
[[ 2, 4, 6],
[ 8, 10, 12],
[14, 16, 18]]
В большинстве случаев метод «dot()» работает быстрее, чем вручную реализованные циклы.
Произведение матриц
Произведение матриц – это более сложная операция, чем сложение или умножение на число. Если у вас есть две матрицы A и B, их можно умножить, если количество столбцов матрицы A равно количеству строк матрицы B. Результатом умножения будет новая матрица C, размерность которой определяется числом строк матрицы A и числом столбцов матрицы B.
Каждый элемент новой матрицы вычисляется как сумма произведений элементов строки первой матрицы на элементы столбца второй матрицы.
Для реализации умножения с использованием циклов приведем следующий пример:
matrix1 = [[1, 2], [3, 4]]
matrix2 = [[5, 6], [7, 8]]
result = [[0, 0], [0, 0]]
for i in range(len(matrix1)):
for j in range(len(matrix2[0])):
for k in range(len(matrix2)):
result[i][j] += matrix1[i][k] * matrix2[k][j]
print(result)
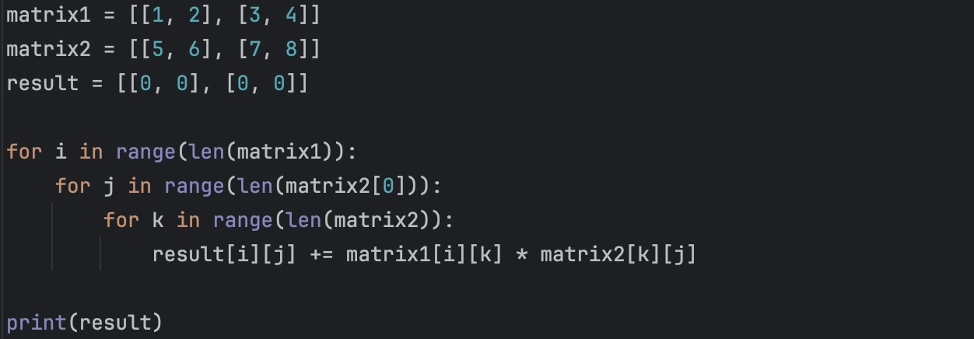
Вывод:
[[19, 22], [43, 50]]

В NumPy для матричного умножения используется метод «dot()»:
import numpy as np
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])
result = np.dot(matrix1, matrix2)
print(result)
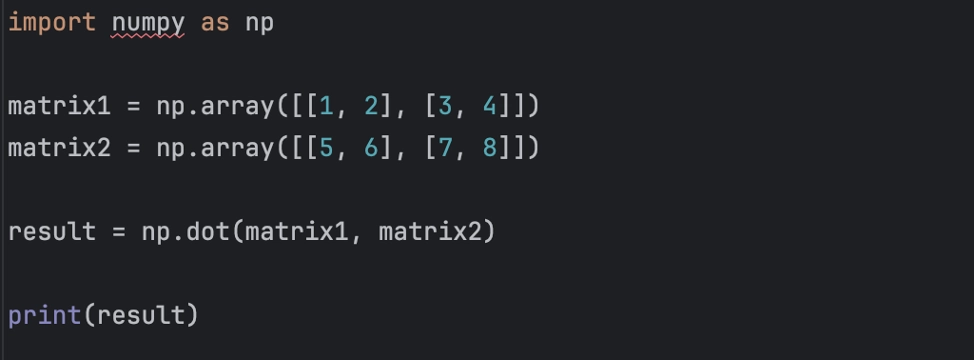
Вывод:
[[19 22]
[43 50]]
Аналогичным образом работает оператор «@»:
import numpy as np
matrix1 = np.array([[1, 2], [3, 4]])
matrix2 = np.array([[5, 6], [7, 8]])
result = matrix1 @ matrix2
print(result)
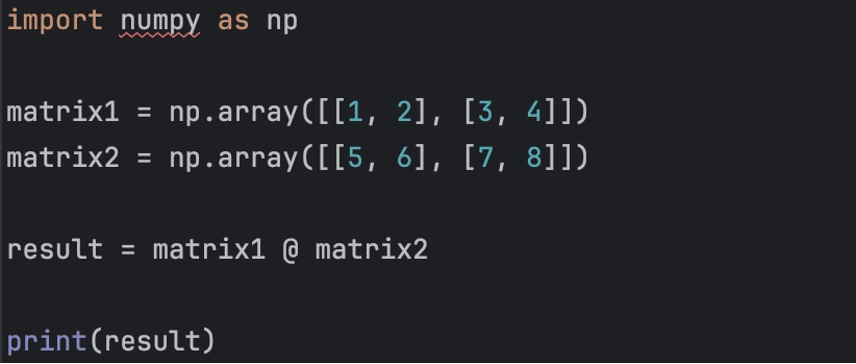
Вывод:
[[19 22]
[43 50]]
Использование метода «dot()» или оператора «@» обеспечивает более быстрый результат по сравнению с ручной реализацией циклов.
Важно помнить, что произведение матриц некоммутативно, то есть изменение порядка умножения приведет к различным результатам.
Транспонирование матрицы
Транспонирование представляет собой операцию, при которой строки и столбцы меняются местами. То есть, первая строка становится первым столбцом, вторая строка – вторым столбцом и так далее.
Если у вас есть матрица A с размерами m x n, то транспонированная матрица, обозначаемая как A^T, будет иметь размеры n x m, и элементы A^T[i][j] будут равны элементам A[j][i].
В Python транспонирование можно осуществить с использованием свойства «T» или метода «transpose()» из библиотеки NumPy.
Пример транспонирования с использованием свойства «T»:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
result = matrix.T
print(result)

Вывод:
[[1 4 7]
[2 5 8]
[3 6 9]]
Также можно воспользоваться методом «transpose()»:
import numpy as np
matrix = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
result = np.transpose(matrix)
print(result)

Вывод:
[[1 4 7]
[2 5 8]
[3 6 9]]
В обоих случаях результат одинаков.
Транспонирование с использованием цикла может быть реализовано следующим образом:
matrix = [[1, 2, 3], [4, 5, 6], [7, 8, 9]]
result = [[0, 0, 0], [0, 0, 0], [0, 0, 0]]
for i in range(len(matrix)):
for j in range(len(matrix[0])):
result[j][i] = matrix[i][j]
print(result)
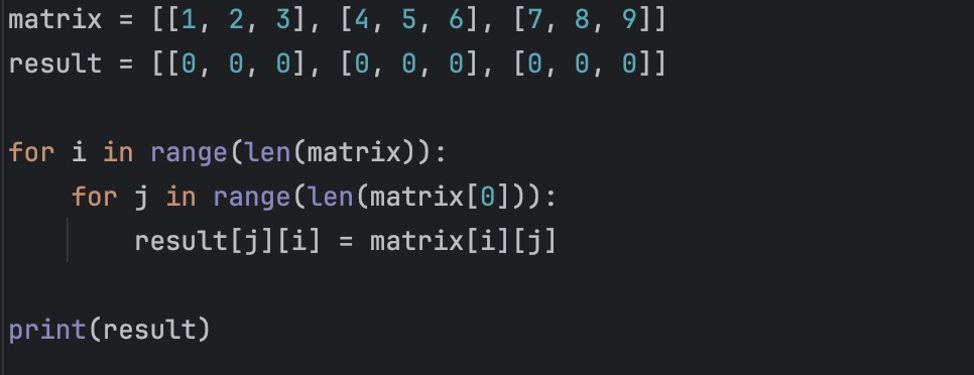
Вывод:
[[1, 4, 7], [2, 5, 8], [3, 6, 9]]

Однако этот метод может быть медленным и неэффективным для больших матриц, поэтому для более быстрого и эффективного решения рекомендуется использовать NumPy.
Нахождение обратной матрицы
Обратная матрица – это такая матрица, которая при умножении на исходную матрицу дает единичную матрицу, где у диагонали стоят единицы, а в остальных ячейках - нули.
В Python обратную матрицу можно найти с использованием метода «inv()» из библиотеки NumPy.
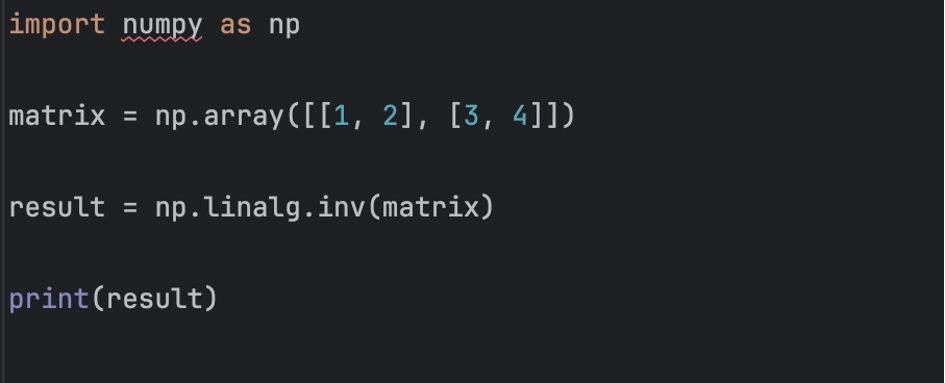
Пример:
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
result = np.linalg.inv(matrix)
print(result)
Вывод:
[[-2. 1. ]
[ 1.5 -0.5]]
Если матрица не имеет обратной матрицы, то метод «inv()» вызовет исключение «LinAlgError: Singular matrix».
Чтобы проверить, имеет ли матрица обратную, можно использовать метод «det()» из библиотеки NumPy, который возвращает определитель матрицы. Если определитель равен нулю, то матрица вырожденная, а потому у нее нет обратной матрицы:
import numpy as np
matrix = np.array([[1, 2], [3, 4]])
determinant = np.linalg.det(matrix)
if determinant == 0:
print("Матрица не имеет обратной матрицы.")
else:
result = np.linalg.inv(matrix)
print(result)

Нахождение обратной Python матрицы с использованием циклов может быть сложным и трудоемким процессом, особенно для больших матриц. Поэтому рекомендуется использовать NumPy.
Заключение
В этой статье мы рассмотрели основные операции с матрицами в Python: сложение, вычитание, умножение на число, умножение матриц и транспонирование. Эти операции очень важные для различных областей, включая линейную алгебру, статистику, физику и информатику.
Операции с матрицами находят широкое применение в решении задач и алгоритмах, которые используются в машинном обучении, компьютерной графике и других сферах. А такие библиотеки, как NumPy, предоставляют удобные инструменты для работы с матрицами в Python, делая код более читаемым и эффективным.